Bien, al asunto pues.¿Cuantos números primos hay?Quizá sería buena idea refrescar la memoria:un número primo es aquel que es divisible solamente por sí mimo y la unidad.Así, 5 es un número primo, pues es solamente divisible por sí mismo y la unidad.4 NO es primo, porque aparte de por sí mismo y la unidad, también es divisible por 2.
Una vez definido los números primos, queda la cuestión de su cantidad.¿Son infinitos o finitos, y en este caso, cuántos son?Bueno, la respuesta nos fue dada por Euclides, en una de las mejores demostraciones de las matematicas, como ya he dicho, y la resupesta es que los numeros primos son infinitos.Sin más preámbulo, allá va:
Primero, vamos a suponer que los numeros primos son finitos.Esto es, suponemos que hay un número determinado de primos, y a partir del último no encontramos ninguno más.Entonces, partiendo de esta premisa, y siguiendo unos pasos lógicos, vamos a llegar a una contradicción, a un absurdo.Como asumir la veracidad de la premisa nos lelva a un absurdo, debemos concluir que la premisa es falsa, y su contraria, (que los numeros primos son infinitos) es verdadera.Vamos a ello:
Supongamos que los numeros primos son finitos, supongamos que en total existen n primos.Podráimos darle un nombre a cada primo:Al primero le llamamos p1, al segundo p2, al tercero p3, y así sucesivamente hasta lelgar al último primo pn.Supongamos que ya hemos hecho esto.Ahora, construyamos el numero siguiente, al que llamaremos N, y que es
 Es decir, calculamos el producto de los n primos y sumamos 1 al resultado.Ahora, vamos a ir dividiendo N entre todos los primos, uno por uno, y comprobamos si el resultado es entero:
Es decir, calculamos el producto de los n primos y sumamos 1 al resultado.Ahora, vamos a ir dividiendo N entre todos los primos, uno por uno, y comprobamos si el resultado es entero: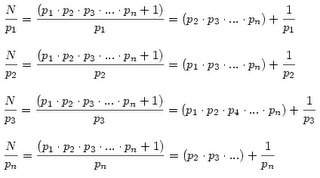
Vemos que en todos los casos por cociente tenemos un entero, el producto de todos los primos menos por el que estamos dividiendo, mas un término del tipo 1/pn, que evidentemente no es entero:ninguno de los cocientes de arriba es entero.Por tanto, N no es divisible por ningún primo.Solamente es divisible por si mismo, y la unidad*.Luego N es, segun la definicion anterior, un numero primo.Pero habiamos supuesto que en nuestra lista p1, p2, p3...pn estaban todos los primos.Obtenemos así una contradicción .Por tanto, como dijimos antes, nuestra premisa inicial es falsa y su contraria (hay infinitos números primos) es verdadera. Y ya hemos acabado.
La demostración parece larga, pero en realidad no lo es tanto, he aprovechado también para definir los numeros primos y para explicar las bases de la demostración por reducción al absurdo.
Espero que os haya resultado interesante.Me parece escandaloso que en las escuelas la gente estudie quién fue el autor de los Milagros de Nuestra Señora y ni siquiera se mencione esta joya de las matematicas.Pero ¿de qué me quejo? A quien no le interese dará igual que se lo hagan estudiar, y a quien le interese casi seguro que acabará encontrándolo por si solo ;).
Un saludo de Smaigol.Espero poder traeros más articulos, y que no sean un tostón :P
*Si un numero no es divisible por ninguno de los primos inferiores a el, tampoco lo es por ningun numero inferior a el, ya que cualquiera de estos numeros puede expresarse como producto de factores primos.
**La "auténtica" demostración de Euclides es ligeramente distinta a la versión que doy aquí.Creo que esta es más fácil de entender para el lector ocasional.
EDIT:Me han comentado que las formulas "en sucio" no se veian muy bien.Así que aquí las tenéis, en rutilante LaTeX:D.Gracias a www.foro.migui.com por hacer esto posible :P

17 comentarios:
Debido a más de 9 años sin estudiar matemáticas...reconozco que no acabo de ver el asunto...también puede ser porque he comido hace un rato y estoy amodorrada...tendré que verlo con más calma...
Imagínate que tienes el número primo más grande posible. Por poner un ejemplo, supongamos que 5 es el mayor número primo que existe.
Ahora multiplica todos los números primos que se supone que existen (2, 3 y 5) y súmale 1 al resultado. (2·3·5)+1=31. Ese número es evidentemente mayor que 5, ya que éste fue uno de los factores del producto.
Ese nuevo número (31) no es divisible por 2. En el producto 2·3·5 el número 2 es un factor, así que al sumar 1 hacemos que no pueda ser divisible por 2. Ésta es la clave del razonamiento.
31 tampoco es divisible por 3, el razonamiento es el mismo. Y tampoco es divisible por 5, nuevamente por culpa del 1 que hemos sumado.
Lo mismo te va a pasar con todos los números hasta 30 que pruebes, 31 no va a ser divisible por ninguno. Por lo tanto, o nuestro número 31 es primo o tiene divisores primos mayores que el mayor primo posible considerado (5).
En cualquiera de los dos casos anteriores, 5 no puede ser el número primo más grande. Para cualquier número que utilices podrás utilizar este razonamiento. Ergo, hay infinitos primos.
Te lo habría explicado yo pero este cubo tetradimensional es muy rapido :D Muchas gracias Tesseract.
Jeje... ;)
Aun así, habré sido rápido, pero he cometido un fallito. Sobra una frase en mi explicación, la primera del quinto párrafo.
Muchisimas gracias...ya lo entiendo...con el ejemplo me ha quedado mucho más claro....Es lo que tiene tener el cerebro medio vegetativo...jeje
Tesseract dijo:
"Aun así, habré sido rápido, pero he cometido un fallito. Sobra una frase en mi explicación, la primera del quinto párrafo. "
Si lo dices porque lo que dijiste implica que 31 no es divisible por 1...eso es hilar demasiado fino para mí XD no creo que nadie se haya fiajdo...
De na, maeglin, a mí también me ayuda ver estas cosas con numeritos. :P
Smaigol, digo que sobra la frase porque debemos detenernos al probar el supuestamente mayor primo posible. Vamos, que al construir el famoso producto (2·3·5)+1 sólo aseguramos que ese número no va a ser divisible por 2, 3 y 5, y tal como yo lo he puesto parece que hay que probar todos los números hasta 30.
Un ejemplito, que ya sé que no te va a hacer falta, pero ya que me he puesto a hacer el idiota con la calcu de Güindous lo pongo: el número 30031 es el resultado de (2·3·5·7·11·13)+1, y no es primo (es divisible por 59).
Oye, y muy bien elegido el tema del artículo. Recuerdo que leí esta demostración de chaval y me quedé flipado.
Ahh ok no caia.Pues es cierto, de hecho en su momento cuando escribí la entrada decidí no poner ejemplos para que no viniera algún listillo con lo que tú dices.Gracias por la aclaración ;)
No entiendo el comentario del número 30031. Por construcción debería ser primo y ¿no lo es? ¿Dónde me he perdido?
No, no tiene por qué ser primo, a eso me refería. 30031 es igual a (2·3·5·7·11·13)+1. Lo único que nos asegura esa descomposición es que 30031 no es divisible por 2, 3, 5, 7, 11 y 13, pero puede ser divisible por algún número mayor.
Hola: necesito en la Universidad exponer ésto, pero no te entiendo en algo...
Osea 30031 es igual a (2·3·5·7·11·13)+1, no significa que sea primo, entonces ¿cómo aseguramos que hay número infitos de primos?
otaivin comparto tu moción por la demostraciion pero te has confundido con lo de pi, en realirar un corolario (o u aparte de el) del teorema de la infinidad de primos dice que raiz de 2 es irracional. solo para aclarar dudas...
para camilo-alejandro:
al 30031 lo consrtuist con
(2x3x5..x13)+1 y encontrast q es divisible por 59 no? pero no por los primos del 2 al 13.despues ponele que tomas
(2x3x4..x17)+1= 510511 es divisuble por 19 y asi seguis agregando primos y siempre va a ser divisible el resultad..pero por un primo que no habias llegado entonces siempre vas a tener un primo mas grande de los que usaste en la multiplicacion
nerdssssssssss
Publicar un comentario