Bien, al asunto pues.¿Cuantos números primos hay?Quizá sería buena idea refrescar la memoria:un número primo es aquel que es divisible solamente por sí mimo y la unidad.Así, 5 es un número primo, pues es solamente divisible por sí mismo y la unidad.4 NO es primo, porque aparte de por sí mismo y la unidad, también es divisible por 2.
Una vez definido los números primos, queda la cuestión de su cantidad.¿Son infinitos o finitos, y en este caso, cuántos son?Bueno, la respuesta nos fue dada por Euclides, en una de las mejores demostraciones de las matematicas, como ya he dicho, y la resupesta es que los numeros primos son infinitos.Sin más preámbulo, allá va:
Primero, vamos a suponer que los numeros primos son finitos.Esto es, suponemos que hay un número determinado de primos, y a partir del último no encontramos ninguno más.Entonces, partiendo de esta premisa, y siguiendo unos pasos lógicos, vamos a llegar a una contradicción, a un absurdo.Como asumir la veracidad de la premisa nos lelva a un absurdo, debemos concluir que la premisa es falsa, y su contraria, (que los numeros primos son infinitos) es verdadera.Vamos a ello:
Supongamos que los numeros primos son finitos, supongamos que en total existen n primos.Podráimos darle un nombre a cada primo:Al primero le llamamos p1, al segundo p2, al tercero p3, y así sucesivamente hasta lelgar al último primo pn.Supongamos que ya hemos hecho esto.Ahora, construyamos el numero siguiente, al que llamaremos N, y que es
 Es decir, calculamos el producto de los n primos y sumamos 1 al resultado.Ahora, vamos a ir dividiendo N entre todos los primos, uno por uno, y comprobamos si el resultado es entero:
Es decir, calculamos el producto de los n primos y sumamos 1 al resultado.Ahora, vamos a ir dividiendo N entre todos los primos, uno por uno, y comprobamos si el resultado es entero: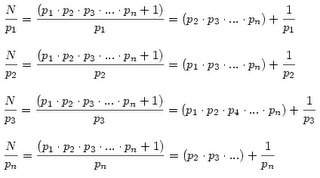
Vemos que en todos los casos por cociente tenemos un entero, el producto de todos los primos menos por el que estamos dividiendo, mas un término del tipo 1/pn, que evidentemente no es entero:ninguno de los cocientes de arriba es entero.Por tanto, N no es divisible por ningún primo.Solamente es divisible por si mismo, y la unidad*.Luego N es, segun la definicion anterior, un numero primo.Pero habiamos supuesto que en nuestra lista p1, p2, p3...pn estaban todos los primos.Obtenemos así una contradicción .Por tanto, como dijimos antes, nuestra premisa inicial es falsa y su contraria (hay infinitos números primos) es verdadera. Y ya hemos acabado.
La demostración parece larga, pero en realidad no lo es tanto, he aprovechado también para definir los numeros primos y para explicar las bases de la demostración por reducción al absurdo.
Espero que os haya resultado interesante.Me parece escandaloso que en las escuelas la gente estudie quién fue el autor de los Milagros de Nuestra Señora y ni siquiera se mencione esta joya de las matematicas.Pero ¿de qué me quejo? A quien no le interese dará igual que se lo hagan estudiar, y a quien le interese casi seguro que acabará encontrándolo por si solo ;).
Un saludo de Smaigol.Espero poder traeros más articulos, y que no sean un tostón :P
*Si un numero no es divisible por ninguno de los primos inferiores a el, tampoco lo es por ningun numero inferior a el, ya que cualquiera de estos numeros puede expresarse como producto de factores primos.
**La "auténtica" demostración de Euclides es ligeramente distinta a la versión que doy aquí.Creo que esta es más fácil de entender para el lector ocasional.
EDIT:Me han comentado que las formulas "en sucio" no se veian muy bien.Así que aquí las tenéis, en rutilante LaTeX:D.Gracias a www.foro.migui.com por hacer esto posible :P
