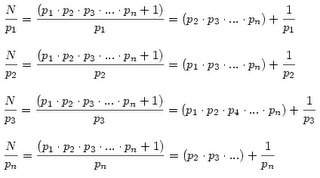Los decimales de pi

A raiz de la entrada anterior, se planteó en el Foro de Migui (concretamente aquí) la cuestión de si los decimales de pi (o de cualquier otro numero trascendente en general) podrían contener todo lo que el mono es capaz de escribir.Uno podría inventarse una codificación de las letras, de manera que una secuencia de letras se convierta en una secuencia de numeros.Por ejemplo, si definimos la sencilla relación a=01, b=02, c=03, d=04, l=12, o=16...encontramos que la palabra "blog" se puede escribir como 02121607 .Si encontramos en los decimales de pi la secuencia "02121607" diríamos que pi tiene escrita la palabra "blog".A partir de este punto, y aplicando el razonamiento del mono, parece que podríamos llegar a la conclusión de que toda la información del universo (y algo más) está contenida en los decimales de pi, dado que pi posee infinitos decimales.

Pero hay una trampa ;).Nuestra razonamiento se realizó bajo la suposición de que el mono escribía aleatoriamente, en todo momento existía la misma probabilidad de que pulsase cada tecla.En los decimales de pi, y usando nuestro anterior código, esto se traduce en que cada pareja de decimales desde 00 hasta 99 tenga la misma probabilidad de aparecer*.¿Es esto cierto? ¿Por qué deberíamos suponer que los decimales de pi son aleatorios? A fin de cuentas, pi tiene su origen en la geometría, no en la estadística, no tiene por qué tener una distribución uniforme de decimales.Así que esta tarde decidí resolver la cuestión por la fuerza.He puesto al programa Mathematica a hacer un recuento de los 40000 primeros decimales de pi.Ayer hice lo mismo, pero al final descubrí un error en la programación que lo manda todo a hacer gárgaras.Hoy lo he intentado de nuevo, con el error corregido.Al acabar, me dará una lista de diez números, cada uno representando el número de veces que han aparecido los números 1,2,3...en los 40000 primeros decimales de pi.Si los decimales de pi son realmente aleatorios, los 10 valores deberían ser iguales, en torno a 4000 cada uno.Si no lo son, puede significar o que los decimales de pi no son aleatorios, o que sencillamente necesitamos una muestra más grande apra el experimento (necesitamos un mayor numero de decimales).Estoy esperando a que acabe...

Bien! Por fín tengo el resultado! Y un bonito histograma que da una idea bastante gráfica del asunto:

Ahora, unos cuantos números:

-Nº de veces que aparece el uno:4060--10'2%
-Nº de veces que aparece el dos:3892--9'7%
-Nº de veces que aparece el tres:3971--10%
-Nº de veces que aparece el cuatro:4014--9'9%
-Nº de veces que aparece el cinco:4040--10'1%
-Nº de veces que aparece el seis:4026--10'1%
-Nº de veces que aparece el siete:3977--9'9%
-Nº de veces que aparece el ocho:4032--10'1%
-Nº de veces que aparece el nueve:3998--10%
-Nº de veces que aparece el cero:3989--9'9%

Como se puede ver, parece que los decimales de pi cumplen bastante bien el requisito de estar distribuidos uniformemente.Os pongo aquí otros histogramas, calculados para los valores de p(numero de decimales considerados) p=10,100,1000,10000.Para que comparéis, y veáis cómo la cosa se va haciendo cada vez más uniforme:

Bueno, yo diría que los decimales de pi son bastante aleatorios :).Pero para asegurarme, mañana haré el cálculo con p=1000000.De ser aleatorios los decimales apenas debería haber diferencia de altura entre las barras del histograma. Seguramente el cálculo le tome un tiempo enorme a mi pobre CPU, pero bueno, todo sea por el bien de la ciencia :P. Sin embargo ahora mismo me apostaría unos leros virtuales a que los decimales de pi son aleatorios.Así que cuestión resuelta :).

Un saludo.

P.S:La diversión no acaba aquí :).¿Qué ocurre con los decimales de e, la constante de Mascheroni o cualquier otro numero trascendente que se nos ocurra? Bueno, para el lector que esté interesado en el tema (y que posea el porgrama Mathematica), voy a colgar en la sección de recursos el .nb que usé para hacer las cuentas.Simplemente tenéis que tocar los dos primeros números que aparecen, p es el número de decimales que entrarán en la estadística y n es el número decimal a considerar (pi, e...).Debéis aseguraros de introducir este número mediante una expresión que le permita calcular a Mathematica los decimales que hagan falta (pi y e ya vienen por defecto en Mathematica, y con muchos decimales, así que en estos casos no hace falta).Lo que quiero decir es que si vais a trabajar con la cte. de Euler-Mascheroni no pongáis 5.77... sino una expresión analítica que tenga a esa constante por límite, por ejemplo.

El resultado que obtendréis será un bonito histograma (con el 10 en el lugar del 0), y 10 números que serán el número exacto de veces que apareció cada dígito, en el orden 1,2,3...8,9,0. Sí, el 0 es el último, más por vagancia mía que por otra cosa XD.Quien quiera puede editarlo of course.La idea matemática subyacente es muy sencilla.

*El decir que las parejas 00 a 99 tienen la misma probabilidad de aparecer (1%)equivale a decir que los dígitos individuales tienen cada uno la misma probabilidad de aparecer (10%), ya que así la probabilidad de aparición de una pareja determinada es (1/10)(1/10)=1/100.

EDIT:Tesseract, un colega del foro de MiGUi, me ha prestado una ayuda inestimable con el algoritmo de mi programa, mejorando su rapidez en varios órdenes de magnitud:El caso p=500000, que se muestra abajo, lo realicé en apenas unos minutos con el algoritmo de Tesseract, mientras que el mío hubiera tardado varias horas (el viernes pasado estuvo como 8 h y no acababa).Además , lo hizo sin conocer el lenguaje de Mathematica XD, ¡lo aprendió sobre la marcha!En resumen, muchas gracias, Tesseract.Podeís ver la conversación que tuve con Tesseract en los comentarios de esta misma entrada.En breves sustituiré en la sección de recursos el algoritmo viejo por el nuevo de Tesseract.Por cierto, como se puede ver, las barras están prácticamente a la misma altura, la diferencia de una a otra es de unos pocos pixels.Otra prueba más de que los decimales de pi son aleatorios :).

EDIT 2: En los comentarios sobre este artículo se ha hecho ver que la condición que este proceso estudia y los decimales de pi cumplen (que cada cifra decimal aparece con la misma frecuencia relativa) es una condicion necesaria pero no suficiente para garantizar la aleatoriedad de los decimales de pi; La secuencia 123456789123456789123456789... pasaría este test y obviamente no es aleatoria.Lo que habría que hacer para subsanar esto es comprobar que las parejas 01,02,03...56...78..98..99,00 aparecen todas con igual frecuencia relativa en los decimales de pi, y lo mismo con las ternas 001,002...998,999,000, con las cuaternas 0001...9999,0000 y así.El numero pi cumple todos estos requisitos, como muestran algunos enlaces que podéis encontrar en los comentarios de este artículo.Así que podemos decir sin miedo que es aleatorio, hasta donde sabemos (no hay por el momento un prueba definitiva).

El mono de la máquina de escribir

La probabilidad tiene algunas consecuencias curiosas.

Por ejemplo, se puede demostrar de manera sencilla (y eso es lo que vamos a hacer) que un mono situado frente a una máquina de escribir que se dedique exclusivamente a teclear al azar por los siglos de los siglos (considérese un mono fuertote) eventualmente escribirá cualquier texto que haya sido escrito por la humanidad, amén de otros que nos abrirán las puertas del conocimiento, como el Necronomicón o la receta de la Coca-cola.Sí, como suena.Es algo realmente sencillo de entender:

Primero, he contado el numero de teclas de mi teclado que sería necesario para escribir la mayoría de los mejores textos de la humanidad (aunque algunas perlas de matemáticas y física se perderían), y creo que con 50 bastará (los números, las letras, la barra espaciadora y algunas más).Suponiendo que el monito teclease realmente al azar (esto es algo difícil de conseguir, pero supondremos que el mono lo logra), la probabilidad de que pulse una tecla determinada es de 1/50, uno entre 50 o del 2%, si así resulta más visual.Ahora bien, ¿qué es un texto? Pues básicamente una secuencia de caracteres (letras, numeros y espacios) ordenados de manera que tengan sentido.Ahora veremos que nuestro mono se convierte en literato.

Empecemos con algo sencillo:escribir la palabra "blog".Si el mono teclea al azar, ¿cuál es la probabilidad de que teclee la palabra "blog"?Para simplificar los cálculos, supondremos que el mono escribe bloques separados de 4 letras.Consideraremos que ha escrito dicha palabra cuando en uno de los bloques salga la palabra "blog".En el caso de que quisiéramos obtener un texto de n letras, consideraríamos bloques de n letras.Esto provoca que la probabilidad que obtengamos al final del calculo sea una estimación a la baja, la probabilidad real de que el mono haya escrito lo que queremos que escriba es más alta.

Si la probabilidad de que escriba una letra determinada es de 1/50, la de que escriba 2 letras determinadas es una entre 2500, y la probabilidad de que escriba 4 letras determinadas (p.ej. la palabra blog) es de una entre 50x50x50x50=50^4=31250000.O de un 0.000016%.Por tanto, la probabilidad de que no escriba la plabra blog es del 99.999984%.Por tanto, la probabilidad de que no se haya escrito la palabra tras n bloques es p(n)= 0.999984^n*.Pero esta sucecisón es decreciente :).Calculemos su valor para, digamos, n=15.000.000.Sale p(n)=0.09, es decir, que tras haber escrito 15 millones de bloques (60 millones de caracteres) la probabilidad de que la palabra blog no haya salido en alguno de los bloques es tan sólo del 9%.La generalización a textos más grandes es evidente.

Consideremos, por ejemplo El Quijote, de Cervantes(supongamos que tiene, p.ej. 10000000 de caracteres, aunque esta es una suposicion arbitraria).¿Cuánto tiempo le llevaría a nuestro mono escribir el Quijote, con, digamos, un 99% de probabilidad? Me había propuesto calcularlo usando software como Mathematica, pero para mi sorpresa la respuesta es un número tan extremadamente grande que ni Mathematica puede con el O_O.En todo caso, y para que no me consideréis un chapuzas, os diré que el número está sin lugar a dudas por encima de 10^600000, un 1 seguido de seiscientos mil ceros.Que no es poco, el mono sin duda deberá tener afan tecleador.

Esto puede darnos una idea de la vastedad del infinito:Con suficiente tiempo, podríamos escribir cualquier cosa.La receta del fuego griego.La pueba de la Conjetura de Goldbach.La Teoría Unificada de la física.El diario secreto de Colón.Una narración cronológica de toda la Hsitoria de la Humanidad tremendamente exacta.Las posibilidades serían ilimitadas.

...pero probablemente eso no va a suceder ;). Un saludo.

*Si la probabilidad de un suceso es A, la probabilidad de que se repita es A · A=A^2.La de que se repita 3 veces, A^3, y así sucesivamente.Esto no es sino una forma de una ley fundamental de la probabilidad que dice que si un suceso A tiene probabilidad p(A), y un suceso B, probabilidad p(B), la probabilidad de que ocurran ambos sucesos es p(A)·p(B), suponiendo que sean eventos independientes (que uno no influya sobre el otro).

Aqui va una pequeña entrada curiosa.

Supon que tienes una pelota de pequeño radio, digamos 1.5 cm.Esta pelota está roedada a lo largo de su ecuador por un pequeño hilo, que tendrá la longitud que sea (unos 9.42 cm).Nos preguntamos:¿Cuanto tiene que aumentar el radio de la pelota de manera que el hilo del ecuador mida exactamente un metro más de longitud?Es decir, ¿cuanto debe aumentar el radio para que el hilo del ecuador mida 1 m y 9.42 cm?

Si hacemos las cuentas, veremos que la respuesta es aproxiamdamente 16 cm.Ahora, supongamos que tenemos una esfera del tamaño del sistema solar.Y su ecuador rodeado por un hilo largo.Muy largo.Ahora, nos hacemos la pregunta de antes: :¿Cuanto tiene que aumentar el radio de la pelota de manera que el hilo del ecuador mida exactamente un metro más de longitud?

Uno espera que la respuesta venga dada en micras o así, dado que el incremento que nos piden es tan pequeño comparado con la longitud de la circunferencia y el radio, que son de proporciones cosmicas.Pues la respuesta es que el incremento del radio vuelve a ser 16 cm; si añadimos tan solo un metro al hilo, este podría levantarse 16 cm sobre la esfera.Antinituitivo, ¿verdad?

La explicación está en la linealidad de la forula de la longitud de la circunferencia, que como sabeis es 2 pi r, siendo r el radio del circulo.Al ser lineal esta funcion, si exigimos un incremento de 1 en la longitud de la circunferencia, siempre debemos obtener el mismo incremento en el radio.Os pongo las cuentas con latex aquí:

Como podeis observar, si queremos incrementar en 1 m la longitud de la circunferencia, siempre deberemos aumentar la longitud del radio en 16 cm.Si uno lo piensa es una consecuencia directa de las fórmulas, pero no deja de ser curioso, ¿no?






Un saludo.

¿Cuantos primos hay?

¿Cuantos? Es posible que muchos de los lectores de estos blogs conozcan la respuesta y esperen articulos algo mas avanzados, pero creo que esta demostración es una de las joyas de las matemáticas, y por su simplicidad es accesible a todo el que tenga interes en conocerla.A mí me cautivó en su momento.Y lo sigue haciendo cuando pienso en ella.Una vez leí que una buena demostración debe ser obvia, clara y elegante.La demostración es clara.Y una vez entendida, el asunto parece obvio y la elegancia es innegable.

Bien, al asunto pues.¿Cuantos números primos hay?Quizá sería buena idea refrescar la memoria:un número primo es aquel que es divisible solamente por sí mimo y la unidad.Así, 5 es un número primo, pues es solamente divisible por sí mismo y la unidad.4 NO es primo, porque aparte de por sí mismo y la unidad, también es divisible por 2.

Una vez definido los números primos, queda la cuestión de su cantidad.¿Son infinitos o finitos, y en este caso, cuántos son?Bueno, la respuesta nos fue dada por Euclides, en una de las mejores demostraciones de las matematicas, como ya he dicho, y la resupesta es que los numeros primos son infinitos.Sin más preámbulo, allá va:

Primero, vamos a suponer que los numeros primos son finitos.Esto es, suponemos que hay un número determinado de primos, y a partir del último no encontramos ninguno más.Entonces, partiendo de esta premisa, y siguiendo unos pasos lógicos, vamos a llegar a una contradicción, a un absurdo.Como asumir la veracidad de la premisa nos lelva a un absurdo, debemos concluir que la premisa es falsa, y su contraria, (que los numeros primos son infinitos) es verdadera.Vamos a ello:

Supongamos que los numeros primos son finitos, supongamos que en total existen n primos.Podráimos darle un nombre a cada primo:Al primero le llamamos p1, al segundo p2, al tercero p3, y así sucesivamente hasta lelgar al último primo pn.Supongamos que ya hemos hecho esto.Ahora, construyamos el numero siguiente, al que llamaremos N, y que es

Es decir, calculamos el producto de los n primos y sumamos 1 al resultado.Ahora, vamos a ir dividiendo N entre todos los primos, uno por uno, y comprobamos si el resultado es entero:


Vemos que en todos los casos por cociente tenemos un entero, el producto de todos los primos menos por el que estamos dividiendo, mas un término del tipo 1/pn, que evidentemente no es entero:ninguno de los cocientes de arriba es entero.Por tanto, N no es divisible por ningún primo.Solamente es divisible por si mismo, y la unidad*.Luego N es, segun la definicion anterior, un numero primo.Pero habiamos supuesto que en nuestra lista p1, p2, p3...pn estaban todos los primos.Obtenemos así una contradicción .Por tanto, como dijimos antes, nuestra premisa inicial es falsa y su contraria (hay infinitos números primos) es verdadera. Y ya hemos acabado.

La demostración parece larga, pero en realidad no lo es tanto, he aprovechado también para definir los numeros primos y para explicar las bases de la demostración por reducción al absurdo.

Espero que os haya resultado interesante.Me parece escandaloso que en las escuelas la gente estudie quién fue el autor de los Milagros de Nuestra Señora y ni siquiera se mencione esta joya de las matematicas.Pero ¿de qué me quejo? A quien no le interese dará igual que se lo hagan estudiar, y a quien le interese casi seguro que acabará encontrándolo por si solo ;).

Un saludo de Smaigol.Espero poder traeros más articulos, y que no sean un tostón :P



*Si un numero no es divisible por ninguno de los primos inferiores a el, tampoco lo es por ningun numero inferior a el, ya que cualquiera de estos numeros puede expresarse como producto de factores primos.

**La "auténtica" demostración de Euclides es ligeramente distinta a la versión que doy aquí.Creo que esta es más fácil de entender para el lector ocasional.

EDIT:Me han comentado que las formulas "en sucio" no se veian muy bien.Así que aquí las tenéis, en rutilante LaTeX:D.Gracias a www.foro.migui.com por hacer esto posible :P

Un saludo y manos a la obra!

¡Hola a todoos! :D

Parece que voy a ser el primero en escribir un artículo en el blog de Matemáticas, y espero que pronto se añadan muchos más, tanto al de Mates como a los otros blogs.También espero que os resulte interesante el artículo, el tema es curioso y poco conocido.

Se trata de lo que en inglés se conoce como "Sphere eversion", y que básicamente consiste en, dada una esfera, conseguir darle la vuelta sin practicar ningún corte en su superficie.Para que nos entendamos, imagina un balón de fútbol.Sin hacerle un corte y sin practicarle agujero alguno, ¿podrías darle la vuelta, es decir, que la cara de dentro acabase fuera y viceversa?
Seguramente estés pensando que esto es imposible.Y efectivamente lo es, al menos en el mundo real.Sin embargo, ocurre que en el mundo de los matemáticos las reglas son algo distintas: Aunque se prohíbe hacer cortes o agujeros en la esfera, ésta puede estirarse todo lo que se quiera, como si fuera de goma, y atravesarse a sí misma.

Puede que en este punto alguien un poco avispado esté pensando que entonces el problema es trivial, pues bastaría con "agarrar" el hemisferio sur de la esfera y empujarlo a traves del interior de la misma para que atravesase el hemisferio norte vuelto del revés.Pero eso no es darle la vuelta a la esfera.Lo que nos queda es más o menos la figura que aparece en el link:

http://www.geom.uiuc.edu/docs/ outreach/oi/Frames/tiff/ 01/1.6/290.comp.tiff

Ese saliente en el ecuador no puede ser eliminado sin cortar la esfera.Así que este método no vale.¿Cual es, pues la solución?

Hay varias, pero ninguna anterior a 1950.Es un problema complicado.Y si es difícil de resolver, aun lo es más de visualizar.Juzgad vosotros mismos:

http://www.geom.uiuc.edu/docs/outreach/oi/evert.mpg

¿Chungo, eh? Yo aún no he sido capaz de visualizar todo el proceso.Solamente fijaos en que se cumplen las reglas: no hay cortes ni agujeros, sólo deformaciones y autointersecciones.

Introduzcámonos algo más en el formalismo matemático.Matemáticamente, ¿qué estamos haciendo al deformar así la esfera?Pues lo que se denomina una homotopía.Quien sepa algo de griego habráintuido el significado de esta palabra: Homo significa "igual" y topos, "lugar".Por tanto "homotopía" vendría a significar "lugares iguales o equivalentes": La homotopía es una relación entre dos curvas del plano o dos superficies del espacio de manera que se conservan todas las características topológicas (entre las que se encuentran los agujeros, nudos...).Por ejemplo, uno puede deformar un círculo en una elipse mediante una homotopía, pero no se puede transformar una esfera en un donut (si la esfera no tiene agujeros, y la homotopia conserva esta caracteristica, no podemos llegar a obtener una figura con agujeros).Ahora quedará claro por qué no podíamos realizar agujeros al intentar invertir la esfera:De haber sido capaces de hacer agujeros, podríamos haber cambiado una propiedad topológica (el numero de agujeros) que una homotopía no puede cambiar.

Para los que estén interesados en el auténtico formalismo, una homotopía entre dos curvas f y g(variedades k-dimensionales, con k R^n diferenciable en cada punto tal que F(s,0)=f y F(s,1)=g.Aquí, s es un punto de [0,1]^k.En otras palabras, F es una función tal que cuando el parámetro t vale 0 se reduce a la función f y cuando t vale 1 se reduce a g.Podemos identificar t con el tiempo.En este sentido, la función F viene a ser como una película:Cada valor de t entre 0 y 1 nos da un "fotograma" del proceso de deformación.Si hiciéramos una animación con las curvas correspondientes a todos los valores de t como fotogramas, veríamos el proceso de deformación de la curva f en g como si de una película se tratase.En circunstancias, dependiendo de la homotopía, puede que f y g incluso sean variedades de distinta dimensión (por ejemplo, existe una homotopía entre el toro y el círculo).

Bueno, ahí queda mi primer artículo :).Espero que no haya sido demasiado pesado.Antes de acabar, un par de referencias:

http://mathworld.wolfram.com/Homotopic.html : Aquí tenéis una animación de la homotopía entre el toro y el círculo.

http://www.geom.uiuc.edu/docs/outreach/oi/: Excelente página divulgativa sobre la inversdión de la esfera.La animación que os he puesto antes proviene de aquí.Pega:Está en inglés :(

Un saludo.